PROCESOS DE RAZONAMIENTO EN CONTEXTO MATEMÁTICO: CARACTERIZACIÓN Y APORTE A LA DIFICULTAD DE LOS ÍTEMS
PROCESSES OF REASONING IN A MATHEMATICAL CONTEXT: CHARACTERIZING AND CONTRIBUTION TO ITEMS DIFFICULTY

 Rojas-Torres, Luis
Rojas-Torres, Luis
Universidad de Costa Rica, Costa Rica

 Jiménez Alfaro, Karol
Jiménez Alfaro, Karol
Universidad de Costa Rica, Costa Rica

 Ordóñez Lacayo, Kenner
Ordóñez Lacayo, Kenner
Universidad de Costa Rica, Costa Rica

 Valverde García, Marisela
Valverde García, Marisela
Universidad de Costa Rica, Costa Rica

 Rojas Rojas, Guaner
Rojas Rojas, Guaner
Universidad de Costa Rica, Costa Rica
CÓMO CITAR:
Rojas-Torres, L., Jiménez Alfaro, K., Ordóñez Lacayo, K., Valverde García, M., & Rojas Rojas, G. (2023). Procesos de razonamiento en contexto matemático: caracterización y aporte a la dificultad de los ítems. Revista de Investigación y Evaluación Educativa, 10((2), 8-23. https://doi.org/10.47554/revie.vol10.num2.2023.pp8-23
Recibido: 2023/04/25
Aceptado: 2023/07/05
Publicado: 2023/08/02
RESUMEN
El objetivo de este trabajo es caracterizar los procesos de razonamiento en contexto matemático presentes en una prueba estandarizada y determinar cuáles de ellos se asocian significativamente con la dificultad de los ítems. Los procesos de razonamiento se determinaron a partir del análisis de soluciones de ítems de RCM, realizado por cuatro personas expertas en educación matemática. El estudio de la relación de los procesos con la dificultad se realizó con un modelo LLTM (n=12800). Los procesos con mayor nivel de asociación con la dificultad fueron: a) identificar una regla de formación en formato de función, b) construcción de contraejemplos o c) verificar el cumplimiento de una regla. Este trabajo es relevante porque permite aproximar la dificultad de los reactivos de RCM antes de una evaluación, utilizando únicamente los procesos de razonamiento requeridos.
ABSTRACT
This work is mainly concerned with characterizing processes of reasoning in a mathematical context of a standardized test and determining which of them are significantly associated with the difficulty of items. These processes were determined by the analysis of RMC item solutions, carried out by four experts in mathematics education. The analysis of the relationship between the processes and the difficulty was carried out with an LLTM model (n=12800). The processes with most association level on the difficulty were the following: a) identifying a formation rule in function format, b) construction of counterexamples and c) verifying a rule compliance. This work is relevant because it allows to approximate the difficulty of the RCM items before an evaluation, using only the required reasoning processes.
PALABRAS CLAVE
Cognición, evaluación, matemáticas, psicometría, razonamiento.
KEYWORDS
Assessment, cognition, mathematics, psychometrics, reasoning.
1. INTRODUCCIÓN
El razonamiento en contexto matemático (RCM) se define como el desarrollo de una heurística apropiada de solución para la resolución de un problema con contenido matemático básico (Jiménez et al., 2018). Este tipo de razonamiento es muy utilizado en las pruebas de admisión a diferentes instituciones educativas, por ejemplo, en la Prueba de Aptitud Académica (PAA) de la Universidad de Costa Rica, la PAA del College Board o el Graduate Record Examination (GRE) del Educational Testing Service (ETS). En estas pruebas el constructo recibe diferentes nombres, pero tienen una esencia muy similar, aunque varían en el nivel de conocimiento matemático utilizado (Dwyer et al., 2003).
El RCM es de mucha utilidad para la selección de estudiantes a programas de estudio debido a que involucra procesos de construcción de estrategias de solución de problemas y recuperación de conocimientos básicos, los cuales son fundamentales para muchos programas de estudio (Rado, Salinas y Rosas, 2016; Virkki, 2022). Esto se puede apreciar mucho mejor en los valores predictivos de este constructo en las notas de diversos cursos (Cabana Yupanqui, 2018; Jiménez & Morales, 2010; Rojas, 2013; Rojas et al., 2018; Sura-Fonseca et al., 2021; Vista y Alkhadim, 2022).
Ahora bien, dada la importancia que ha adquirido el constructo de RCM, resulta relevante analizar si el constructo pretendido es bien evaluado por las pruebas usuarias. Una fuente de evidencia asociada a que los ítems evalúan un constructo pretendido es que las tareas demandadas por el constructo sean las determinantes principales de la dificultad de los reactivos. Es esperable que la dificultad del ítem dependa mayormente de factores propios del constructo, que de variables ajenas a este. Por ejemplo, en una prueba de aritmética básica, la dificultad de los ítems debe depender de la cantidad y tipo de operaciones presentes, en lugar de elementos asociados a comprensión de lectura o a presencia de operaciones fuera de las consideradas.
En el caso de las pruebas que evalúan RCM se debe velar porque estas no basen su dificultad en factores ajenos al constructo como la extensión de los cálculos, la especificidad de los contenidos matemáticos o la complejidad de la redacción de los problemas, los cuales son factores de varianza irrelevante al constructo (AERA et al., 2014).
Dada la importancia de examinar si los factores propios constructos determinan la dificultad de los reactivos, junto con la examinación de que los factores ajenos no afecten la dificultad, resulta relevante plantear modelos estadísticos que evalúen el aporte de estos factores a la dificultad, para así determinar si los factores propios del constructo son los principales responsables de la dificultad.
En función de lo anterior, el objetivo de este trabajo es caracterizar los procesos de RCM de una prueba particular e identificar aquellos que se asocian significativamente con la dificultad de los ítems de esta prueba.
1.1. PROCESOS ASOCIADOS A LA DIFICULTAD DE ÍTEMS DE RCM
Según las Bases de la Revisión y la Actualización Curricular, el término «enfoque» se presenta de la siguiente manera:
El análisis del aporte de las características de un ítem o de los procesos de razonamiento a la dificultad de los ítems generalmente se examina con la técnica de Modelo Logístico Lineal del Test (LLTM, por sus siglas en inglés). Este análisis demanda la construcción de una matriz de atributos de los ítems, lo cual demanda una caracterización muy precisa de los procesos de resolución demandados por los reactivos. Este procedimiento es difícil cuando se trabaja con constructos tan complejos como el RCM, dado que los procesos utilizados para la solución de los ítems son muy variados. Debido a esto, el análisis LLTM se trabaja generalmente con constructos muy delimitados como operaciones con enteros, operaciones lógicas o análisis de patrones (Wilson et al., 2006). En la revisión de literatura solo se encontraron dos análisis LLTM en constructos similares al RCM.
En Rojas-Torres (2013) se observó que los atributos o procesos de los ítems asociados positivamente con la dificultad de los ítems de una prueba que evalúa razonamiento con contenido matemático fueron: elementos algebraicos, nivel del contenido matemático y organizar la información en una fórmula o relación matemática; en cambio, los procesos deductivos e inductivos estuvieron asociados a la facilidad.
Por su parte, Embretson & Daniel (2008) encontraron que los procesos asociados positivamente con la dificultad de los ítems en el GRE fueron: generación de un diagrama, integrar la información en una ecuación (llamado generar una nueva ecuación), traducir una ecuación textual a lenguaje matemático y el análisis de opciones. En este caso, los atributos asociados al nivel de contenido matemático no estuvieron asociados a la dificultad.
Por su parte, Embretson & Daniel (2008) encontraron que los procesos asociados positivamente con la dificultad de los ítems en el GRE fueron: generación de un diagrama, integrar la información en una ecuación (llamado generar una nueva ecuación), traducir una ecuación textual a lenguaje matemático y el análisis de opciones. En este caso, los atributos asociados al nivel de contenido matemático no estuvieron asociados a la dificultad.
1.2. BENEFICIOS DEL ANÁLISIS DE RELACIÓN DE LOS ATRIBUTOS CON LA DIFICULTAD DE LOS ÍTEMS
El mayor beneficio de cuantificar la asociación entre atributos y dificultad de los ítems radica en que permite determinar los aspectos del constructo que se manifiestan en las puntuaciones. Muchas veces se utilizan aspectos de los constructos que no se reflejan en las puntuaciones, hecho que implica que el constructo no sea evaluado apropiadamente. Luego de un análisis de atributos, se puede incentivar a los constructores de ítems a que utilicen con mayor frecuencia los atributos relevantes, para así garantizar que la prueba mida el constructo definido teóricamente. Por otro lado, se puede analizar si los atributos poco relevantes se están utilizando correctamente y se pueden buscar nuevas formas de incluirlos en las pruebas.
Otro beneficio es que la cuantificación de los aportes de los atributos a la dificultad brinda una fórmula para calcular la dificultad de los reactivos. Esta fórmula brinda un criterio objetivo para determinar la dificultad de un ítem antes de aplicarlo a una población. De esta manera, se puede evitar construir una prueba con una dificultad no deseada, que genera una cadena de consecuencias contraproducentes para la medición (Hamamoto et al., 2020).
Por último, se puede determinar si algún atributo de contenido o formato ajeno al constructo está contribuyendo excesivamente a la dificultad. La identificación de los atributos es trascendental para asegurar que las puntuaciones reflejen el constructo, en lugar del manejo de condiciones ajenas al constructo. Una forma de controlar la influencia de un atributo de este tipo es homogeneizar su presencia en los ítems.
Por tanto, en vista de estos beneficios y de la importancia que tienen las pruebas de RCM, resulta relevante analizar cuáles procesos de razonamiento presentes en los ítems efectivamente explican la dificultad de estos.
2.MÉTODO
Dada la naturaleza de las variables de interés de estudio, esta investigación se enmarca en el enfoque cuantitativo. El alcance del trabajo es correlacional y el diseño es no experimental, de corte transversal (Hernández-Sampieri y Mendoza, 2018).
2.1. PARTICIPANTES
Los participantes del estudio fueron las 12800 personas que realizaron la fórmula 1 de la Prueba de Aptitud Académica (PAA) de la Universidad de Costa Rica (UCR) en el 2019. Este grupo de personas estuvo conformado por 5813 hombres y 6987 mujeres.
2.2. INSTRUMENTOS
El instrumento utilizado fue la Prueba de Aptitud Académica (PAA), la cual estuvo conformada por 75 preguntas de razonamiento, con 35 ítems de RCM. En este estudio se consideraron 31 ítems de RCM; se prescindió de dos ítems porque presentaron correlaciones ítem-total inferiores a 0.20 y se prescindió de otros dos, debido a que los jueces no lograron un consenso respecto a los atributos presentes en estos reactivos. El alfa de Cronbach del grupo de 31 ítems fue 0,86.
Las variables del estudio son 13 procesos de razonamiento presentes en los ítems de RCM. También se consideraron cinco atributos del contenido y del formato de dichos reactivos, los cuales son factores potenciales de dificultad y, por ende, deben utilizarse como variables control. Estas 18 variables están codificadas con los valores cero o uno, que indican si el atributo está ausente o presente en el ítem, respectivamente.
La definición de los procesos de razonamiento se presenta en la sección de resultados, debido a que es parte de la investigación realizada. Los atributos de contenido y formato de los ítems considerados fueron:
- Relaciones textuales: atributo que indica si el ítem tiene una relación matemática entre variables escrita en prosa, la cual debe traducirse a texto matemático.
- Conocimiento requerido: señala si la solución del ítem requiere de conocimientos fuera de la aritmética de los números naturales. Este atributo incorpora en el modelo una variable asociada a la complejidad matemática de la solución.
- Extensión larga de texto: este atributo permite identificar los ítems que utilizan cinco o más líneas de texto.
- Complejidad textual: este atributo indica que la información relevante no se presenta como una secuencia de oraciones de estructura simple.
- Negación: atributo que indica que hay una instrucción que incluye una negación (por ejemplo, no, nunca o imposible).
Para la selección de los atributos de contenido y formato se consideraron las particularidades de los ítems de RCM observadas en Brizuela et al. (2014), donde se muestra que las demandas matemáticas o léxicas de los ítems pueden implicar procesos de resolución más complejos. Por otra parte, en Embretson y Daniel (2008), se observó que la cantidad de palabras o la presencia de relaciones algebraicas en formato de prosa, fueron predictores significativos de la dificultad de ítems de RCM.
2.3 PROCEDIMIENTO
La primera etapa del estudio fue la definición de los procesos de razonamiento. Para este trabajo se consideró la clasificación de los ítems de RCM de la PAA, la cual distingue cuatro categorías:
- Generalización: proceso en el que se analiza una secuencia de elementos matemáticos, con el fin de descubrir un patrón implícito en la secuencia.
- Representación: proceso en el que se debe construir y analizar una representación de la información para llegar a la solución del problema.
- Indagación: proceso en el que se deben explorar los datos dados, para encontrar asociaciones o particularidades no evidentes que permitan solucionar el problema.
- Verificación: proceso en el que se analiza la veracidad de proposiciones planteadas en el ítem (Jiménez et al., 2018).
Luego, se seleccionaron seis ítems de cada una de estas categorías, que fueran parte del banco de ítems de la PAA. Seguidamente, cuatro personas expertas en matemática analizaron la solución de los ítems e identificaron y caracterizaron los procesos de razonamiento involucrados en la resolución. Estos procesos no se presentaron en todos los ítems, sino que cada ítem tuvo su combinación particular de procesos.
Después de la definición de los procesos, las personas expertas realizaron un análisis individual de los 31 ítems seleccionados para el análisis LLTM, en el cual debían identificar si los procesos establecidos estaban presentes en los ítems. Para cada proceso se analizó la cantidad de ítems en que las cuatro personas expertas tuvieron un acuerdo total respecto a la presencia del proceso (es decir, se concluyó que había un acuerdo total de la presencia de un proceso en el ítem; si la totalidad de los expertos coincidían en que el proceso estaba presente o ausente). Para cada proceso hubo porcentajes de acuerdo total, sobre la presencia del proceso en los ítems, superiores al 90%.
Es importante mencionar que en el análisis individual de los ítems seleccionados para el LLTM se presentó un proceso que no había aparecido en el primer grupo de ítems. Esto implica que la familia de procesos no puede ser exhaustiva, debido a que los ítems de RCM tienen un componente inherente de creatividad. Asimismo, hubo un proceso de razonamiento que apareció en el primer grupo de ítems que no se manifestó en el segundo bloque.
Finalmente, cuando no hubo acuerdo total sobre la presencia de un proceso de razonamiento en un ítem, las personas expertas realizaron un análisis grupal para decidir si el proceso estaba presente en el reactivo. De esta manera, se construyó la matriz de atributos de los ítems, que es la base para el análisis estadístico.
2.4 ANÁLISIS DE DATOS
El análisis de datos se realizó con el modelo logístico lineal del test (LLTM). Este modelo explica que la probabilidad de acierto de los ítems en función de la presencia de K propiedades en los ítems (W_jk, j El análisis de datos se realizó con el modelo logístico lineal del test (LLTM). Este modelo explica que la probabilidad de acierto de los ítems en función de la presencia de K propiedades en los ítems (W_jk, j número del ítem y k número del atributo) y la habilidad de los sujetos (θ_i). En este modelo se formula que el logit de la probabilidad que tiene el sujeto i de acertar el ítem j, viene dada por
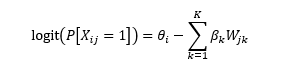
Se puede observar que la fórmula anterior es similar a la fórmula del modelo de Rasch, solo que se busca explicar el parámetro de dificultad Rasch del ítem j (β_j) en función de las K propiedades consideradas. En vista de lo anterior, los coeficientes β_k representan el efecto lineal de los atributos en la dificultad de los ítems (Wilson et al., 2006).
La formulación del modelo LLTM también se puede abordar desde el enfoque de los modelos lineales generalizados mixtos (Bulut et al., 2021; De Boeck et al., 2011). En este caso los coeficientes de regresión de los atributos de los ítems se convierten en efectos fijos y la habilidad de los sujetos en un intercepto aleatorio. Además, la variable dependiente se construye con las respuestas dadas de las 12800 personas a los 31 ítems considerados, lo que implica que la variable dependiente sea un vector de 12800*31=396800 casos. La ventaja de este enfoque es que permite estudiar la varianza de los efectos aleatorios. En este trabajo se utilizó el paquete denominado linear mixed-effects models using eigen and S4 (lme4, Bates et al., 2015) de la plataforma R (R Core Team, 2021) para estimar el modelo mixto asociado al LLTM de interés.
Es importante mencionar que antes de la estimación del modelo LLTM, se analizó la unidimensionalidad del grupo de ítems utilizados, que es el supuesto básico del modelo de estudio. El estudio del supuesto se realizó con el cociente de los autovalores de la matriz de correlaciones de los ítems. El cociente del primer autovalor con el segundo fue de 4,58 unidades y, como dicha razón fue mayor que 4 se concluyó la unidimensionalidad de los datos (Reeve et al., 2007).
Finalmente, para analizar el ajuste del modelo se estimó la correlación de la dificultad de los ítems con el modelo de Rasch y la generada a partir del modelo LLTM.
3.RESULTADOS
3.1. CARACTERIZACIÓN DE LOS PROCESOS DE RAZONAMIENTO
Luego del análisis de jueces, se observó que en el bloque de 31 ítems analizados en este estudio había 13 procesos de razonamiento. A continuación, se presentan las definiciones de los procesos (en el paréntesis aparecen las categorías de RCM a la que están asociados):
- Organizar la información (representación). En este proceso se organiza la información explícita en el ítem en un cuadro, fórmula, dibujo o esquema.
- Inferir con base en la representación (representación). En este proceso se realiza una inferencia, basada en la representación, sobre la operación que debe realizarse para continuar la solución del ítem.
- Completar la representación (representación). En este proceso se integra una representación con un dato adicional o se combinan dos representaciones.
- Generar un dato auxiliar (indagación). En este proceso se debe crear una pieza de información no sugerida por el ítem, que es necesaria para llegar a la solución del problema.
- Utilizar un algoritmo de aproximación (indagación). Este proceso consiste en obtener una solución por medio de una serie ordenada de pasos, dirigida a acotar las posibilidades iniciales de respuesta. Este proceso no apareció en el primer bloque de ítems analizados.
- Determinar los casos implícitos (indagación). En este proceso se deben identificar los casos que cumplen una condición dada, los cuales son necesarios para analizar el problema.
- Analizar el caso extremo (indagación). Este proceso consiste en concluir que la solución del problema se reduce al análisis de un caso extremo, ya sea el valor máximo o el mínimo.
- Análisis directo de las opciones (verificación). Consiste en realizar la operación sugerida por una opción y verificar si esta opción es verdadera.
- Análisis basado en la búsqueda de un contraejemplo (verificación). Consiste en construir un ejemplo que permite invalidar una proposición presente en una opción.
- Probar el cumplimiento de una regla (verificación): Proceso en el que se verifica si una regla implícita o explícita en el ítem se cumple alguna opción (la regla puede ser una propiedad matemática o una condición lógica).
- Identificar una regla de formación recursiva (generalización). Este proceso consiste en reconocer cómo se asocia un término de una secuencia con el término predecesor.
- Identificar una regla dependiente de la posición (generalización). En este proceso se debe determinar cuál es la fórmula que define un término de la secuencia en función de la posición en la secuencia. Este proceso es útil para determinar términos lejanos a los dados.
- Extrapolación del patrón (generalización). Este proceso consiste en determinar un término de la secuencia descrita por medio del uso de la regla encontrada.
El proceso que no apareció en los ítems analizados, pero que sí emergió en el primer bloque de análisis correspondió a la categoría de RCM denominada verificación. Este proceso se nombró análisis exhaustivo de una proposición, consiste en analizar una proposición cuya veracidad demanda del estudio de varios escenarios.
3.2. MODELO LLTM
En la tabla 1 se presentan los resultados del modelo LLTM. Se puede observar que los atributos de contenido y formato que se asocian con la dificultad de los ítems son conocimiento requerido y complejidad textual y el que se asocia con la facilidad es la negación.
TABLA 1.
MODELO LLTM SOBRE LAS DIFICULTADES RASCH DE LOS ÍTEMS DE RCM DE LA PAA
| ATRIBUTO/PROCESO | COEF | ee | z | p |
|---|---|---|---|---|
| Relación textual | -0.264 | 0.014 | 19.086 | 0.000 |
| Conocimiento requerido | 0.587 | 0.017 | -35.446 | 0.000 |
| Larga extensión | 0.134 | 0.012 | -11.339 | 0.000 |
| Complejidad textual | 0.971 | 0.018 | -53.295 | 0.000 |
| Negación | -1.122 | 0.015 | 73.209 | 0.000 | Organizar la información | -0.447 | 0.015 | 29.678 | 0.000 |
| Inferir con base en la representación | 0.468 | 0.017 | -28.006 | 0.000 |
| Completar la representación | 0.548 | 0.014 | -39.826 | 0.000 |
| Generar un dato auxiliar | -0.077 | 0.013 | 5.795 | 0.000 |
| Utilizar un algoritmo de aproximación | 0.665 | 0.017 | -38.674 | 0.000 |
| Determinar los casos implícitos | 0.649 | 0.017 | -38.007 | 0.000 |
| Analizar el caso extremo | 0.087 | 0.019 | -4.456 | 0.000 |
| Análisis directo de las opciones | 0.575 | 0.014 | -39.775 | 0.000 |
| Análisis basado en la búsqueda de un contraejemplo | 2.438 | 0.030 | -81.603 | 0.000 |
| Probar el cumplimiento de una regla | 0.857 | 0.015 | -57.171 | 0.000 |
| Identificar una regla de formación recursiva | 0.098 | 0.019 | -5.279 | 0.000 |
| Identificar una regla dependiente de la posición | 1.429 | 0.031 | -45.817 | 0.000 |
| Extrapolación del patrón | -0.363 | 0.023 | 15.905 | 0.000 |
| Desviación estándar de los interceptos (σ_θ) | 0.995 |
Con respecto a los procesos de la categoría representación, dos de ellos se asocian con la dificultad (inferir con base en la representación y completar la representación) y el otro con la facilidad (organizar la información). En cuanto a la categoría de indagación, dos de los cuatro procesos se asociaron con la dificultad de los ítems (utilizar un algoritmo de aproximación y determinar los casos implícitos), los otros dos no se asociaron con la dificultad ni con la facilidad.
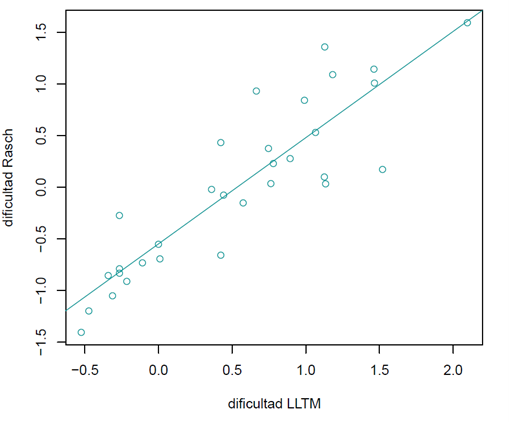
FIGURA 1.
GRÁFICO DE DISPERSIÓN DE LAS DIFICULTADES RASCH Y LAS DIFICULTADES LLTM
En la categoría de verificación todos los procesos se asociaron con la dificultad de los ítems. Finalmente, en la categoría de generalización, solamente uno de los procesos se asoció con la dificultad: identificar una regla dependiente de la posición.
Por otro lado, el modelo LLTM, por medio del enfoque de modelos mixtos, brinda una estimación de la desviación estándar de los interceptos en la fórmula del logit de acierto de un ítem, en este caso, la desviación de las habilidades de los sujetos. Se puede observar que esta desviación es prácticamente 1, esto se debe a que no se consideró ninguna variable específica de los sujetos que capture alguna parte de la variabilidad de las habilidades.
Con respecto al ajuste del modelo, se puede observar que la correlación entre las dificultades del modelo LLTM y el modelo Rasch fue de 0.89, esto indica que hay una muy buena predicción de las dificultades del modelo de Rasch a partir del modelo LLTM. En la figura 1 se muestra el gráfico de dispersión de estas dificultades, en el que se puede observar que los puntos tienen una clara tendencia lineal.
4.DISCUSIÓN
Antes de profundizar en el análisis de la relación individual de los atributos y procesos de razonamiento con la dificultad, hay que mencionar que el conjunto de variables consideradas presenta una gran capacidad explicativa de la dificultad de los ítems, lo cual fue evidenciado por la alta correlación de las dificultades Rasch con las estimadas por el modelo LLTM. Este punto es importante de resaltar porque brinda a los constructores de ítems una fórmula objetiva para estimar la dificultad de los ítems antes de su aplicación.
El punto central de esta discusión es el aporte de los atributos y procesos a la dificultad de los ítems. Con respecto a los atributos de contenido y formato del ítem se observó que la demanda de conocimiento y la complejidad del texto aumentaron la dificultad. Este efecto era muy predecible, debido a que ambos atributos provocan que las personas examinadas realicen procesos cognitivos adicionales como recuperación del conocimiento y comprensión de lectura. De hecho, el efecto del conocimiento ya había sido observado en Rojas-Torres (2013). En vista de estos resultados, se debe analizar cuál es el porcentaje de la dificultad de los ítems derivadas de estos atributos y cuál el porcentaje derivado de los procesos de razonamiento, ya que la dificultad del ítem debe estar basada en estos últimos.
Un aspecto observado en los atributos de contenido y forma fue la facilitación provocada por la negación. En este punto hay que considerar que la presencia de una negación no implica, necesariamente, un aumento de la dificultad en comparación con la ausencia de ella (Wise, 2020); no obstante, la facilitación sí es algo atípico. Una hipótesis para este fenómeno es que este efecto es una compensación por la presencia de otros atributos, ya que en los cuatro ítems en que aparece el proceso de negación hay otros atributos con contribuciones fuertes a la dificultad (de hecho, en uno de los ítems hay tres procesos con aportes a la dificultad mayores a 0.80). En fin, este comportamiento debe ser investigado con más detalle, para corroborar si el efecto observado en este estudio fue una particularidad de los datos o si realmente hay una asociación con la facilidad de los ítems.
En la categoría de representación se observaron dos procesos que aumentaron la dificultad (inferir con base en la representación y completar la representación) y uno que la disminuyó (organizar la información). Se puede observar que los dos procesos que contribuyeron al aumento de la dificultad de los ítems son aquellos en los que se necesita trabajar con la representación construida. Este resultado coincide con el efecto del proceso integrar la información en una ecuación de Embretson y Daniel (2008), ya que esta demanda trabajar con las representaciones preliminares. Por otro lado, el proceso que facilita el ítem es el asociado con la organización de la información, este efecto se puede deber a que es un proceso común en los ítems de matemática de todos los niveles escolares, por lo que en la población meta de la PAA, el proceso ubica a los examinados en un contexto familiar de trabajo.
En cuanto a generalización, se observó que el único proceso utilizado que aporta a la dificultad es la identificación de reglas en función de la posición. En cambio, la identificación de reglas de recursividad no aportó al aumento de la dificultad, esto se puede deber a que estas están limitadas a patrones sencillos, dado que la regla debe ser evidente en cada par de términos adyacentes; mientras que, en las reglas funcionales, cada igualdad puede ser estudiada individualmente, lo que permite mayor complejidad (por ejemplo, f (2) = 4+2; f (3) = 6+3; f (4) =8+4). Lo anterior se relaciona con los resultados obtenidos en Carraher et al. (2008) que indican que los estudiantes tienden a utilizar en mayor medida las reglas recursivas, pues se les dificulta establecer relaciones entre variables (funcionales). De forma similar en Barboza et al. (2012) se encontró que los estudiantes tienen dificultad para encontrar relaciones funcionales y encontrar reglas explícitas adecuadas. No obstante, la aplicación del patrón tampoco se asoció con la dificultad, hecho que puede deberse a que la complejidad del reactivo radica en la identificación de la regla. Investigaciones como la de Barboza et al. (2012) y Ureña (2021) establecen que los alumnos tuvieron dificultades en la exploración de patrones cuando tuvieron que generalizar a valores lejanos y menor dificultad en generalización a valores cercanos.
Además, se obtuvo que todos los procesos de verificación se asociaron con la dificultad de los ítems, este hecho coindice con el resultado de Embretson y Daniel (2008). Este resultado es esperable debido a que involucran mayor trabajo por parte de la persona examinada, ya que debe analizar las cuatro situaciones de las opciones, en lugar de solo la situación expuesta en el encabezado del ítem. En particular, se puede observar que el proceso que más contribuye a la dificultad es búsqueda de un contraejemplo, que puede ser provocado a la novedad del proceso, ya que, en lugar de comprobar una afirmación, se busca argumentar que es falsa.
Por último, en indagación se observaron dos procesos que se asocian con la dificultad: utilizar un algoritmo de aproximación y determinar los casos implícitos; en ambos casos se puede observar que las tareas demandadas no son rutinarias y demandan un nivel de ingenio del individuo. Los otros dos procesos que no aportaron a la dificultad son un poco más familiares y no son ingeniosos: análisis del caso extremo y generar un dato auxiliar.
La principal dificultad de este estudio fue que no existía una teoría exhaustiva que indicara la caracterización de los procesos de razonamiento de los ítems de RCM, no obstante, esto es esperable debido a la gran cantidad de posibilidades que ofrece este constructo. En el caso de la PAA fue posible construir una caracterización de los ítems, debido a que el constructo está bien delimitado en cuanto al contenido matemático, por tanto, estos ítems se centran mucho más en el razonamiento que en algoritmos matemáticos, los cuales pueden complejizar la caracterización del constructo de interés.
Para estudios futuros se sugiere analizar todo el banco de ítem de la PAA para construir una categorización de los procesos de razonamiento, lo más exhaustiva posible. Posteriormente, se puede estimar el análisis LLTM en un conjunto intencionado de ítems de una categoría de razonamiento, en la cual estén presentes todos los procesos de razonamiento. También, se puede realizar una regresión latente -la cual es un modelo LLTM con variables de los individuos- para así predecir el logit de acierto de un ítem con mayor precisión.
En conclusión, este análisis de los procesos de razonamiento brindó evidencia sobre cuáles de ellos están asociados con la dificultad de los ítems de RCM. Ahora les corresponde a los constructores de ítems potenciar el uso de estos procesos para asegurar que la PAA evalúe el constructo pretendido. Además, se deben mitigar los efectos de los atributos de contenido y formato sobre los ítems, esto se puede conseguir si se modifican los pocos ítems que presentaron estas condiciones.
5.FINANCIACIÓN
Este artículo es resultado de la investigación 723-C1-209 Elementos asociados a la dificultad de los ítems de razonamiento en contexto matemático de la Prueba de Aptitud Académica, desde el enfoque de los Modelos Explicativos de Respuesta al Ítem, financiada por la Universidad de Costa Rica.
REFERENCIAS
AERA, APA, & NCME. (2014). Standards for educational and psychological testing.
Bates, D., Machler, M., Bolker, B., & Walker, S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67 (1), 1-48. https://doi.org/10.18637/jss.v067.i01 4
Brizuela, A., Cerdas, D., Fallas, S., Ordóñez, K., Pérez, N., Rojas-Torres, L., & Seas, G. (2014). Resolvamos la PAA.Editorial UCR.
Cabana Yupanqui, S. B. (2018). Análisis predictivo del rendimiento académico en los alumnos de la escuela profesional de ingeniería en informática & sistemas de la UNJBG, utilizando redes neuronales semestre 2017-I. [Tesis para obtener el grado de ingeniero, Universidad Nacional Jorge Basadre Grohmann]. Repositorio de la UNJBG http://repositorio.unjbg.edu.pe/handle/UNJBG/3200
Carraher, D. W, Martínez, M. V., & Schliemann, A. (2008). Early Algebra and mathematical generalization. ZDM Mathematics Education, 40, 3–22.
De Boeck, P., Bakker, M., Zwitser, R., Nivard, M., Hofman, A., Tuerlinckx, F., & Partchev, I. (2011). The Estimation of Item Response Models with the lmer Function from the lme4 Package in R. Journal of Statistical Software, 39 (12), 1-28. https://doi.org/10.18637/jss.v039.i12
Dwyer, C., Gallagher, A., Levin, J., & Morley, M. E. (2003). What is Quantitative Reasoning? Defining the Construct for Assessment Purposes .(RR-03-30; Research Reports). Educational Testing Service.
Embretson, S. E., & Daniel, R. C. (2008). Understanding and quantifying cognitive complexity level in mathematical problem-solving items. Psychology Science Quarterly, 50(3), 328-344.
Hamamoto, P. T., Silva, E., Tosta, Z. M., Marmorato, M., Fernández, D. C., & Bicudo, A. M. (2020). Relationships between Bloom’s taxonomy, judges’ estimation of item difficulty and psychometric properties of items from a progress test: a prospective observational study. Sao Paulo Medical Journal, 138 (1), 33-39. https://doi.org/10.1590/1516-3180.2019.0459.R1.19112019
Hernández-Sampieri, R., & Mendoza, C. (2018). Metodología de la investigación. Las rutas cuantitativa, cualitativa & mixta. Editorial Mc Graw Hill Education.
Jiménez, K., Rojas-Rojas, G., Brizuela, A., & Pérez, N. (2018). Validación de un modelo de cuatro estrategias de resolución de ítems de razonamiento en una prueba estandarizada de selección. Revista Costarricense de Psicología, 37 (1), 77-88. https://doi.org/10.22544/rcps.v37i01.04
R Core Team. (2021). R (versión 4.2.2) [Software de computador]. R Foundation for Statistical Computing. https://cran.r-project.org/bin/windows/base/
Rado, J. M., Salinas, J. W., & Rosas, F. R. (2016). Predicción del rendimiento en el examen de admisión a la UNALM utilizando las técnicas de Análisis Discriminante Lineal & Análisis Discriminante con Algoritmos Genéticos. Anales científicos, 77 (1), 8–16. https://doi.org/10.21704/ac.v77i1.474
Reeve, B.B., Hays, R.D., Bjorner, J.B., Cook, K.F., Crane, P.K., Teresi, J.A., Thissen, D., Revicki, D.A., Weiss, D.J., Hambleton, R.K., Liu, H., Gershon, R., Reise, S.P., Lai, J., & Cella, D. (2007). Psychometric evaluation and calibration of health-related quality of life item banks: plans for the Patient-Reported Outcomes Measurement Information System (PROMIS). Med Care. 45 (5) 2-31. https://doi.org/10.1097/01.mlr.0000250483.85507.04
Rojas, L. (2013). Validez predictiva de los componentes del promedio de admisión a la Universidad de Costa Rica utilizando el género & el tipo de sexo como variables control. Actualidades Investigativas en Educación, 13(1).
Rojas, L., Mora, M., & Ordóñez, G. (2018). Asociación del razonamiento cuantitativo con el rendimiento académico en cursos introductorios de matemática de carreras STEM. Revista digital: Matemática, Educación e Internet, 19 (1). https://doi.org/10.18845/rdmei.v19i1.3851
Rojas-Torres, L. (2013). Predicción de la dificultad de la Prueba de Habilidades Cuantitativas. Revista digital: Matemática, Educación e Internet, 13 (1). https://doi.org/10.18845/rdmei.v13i1.1627
Sura-Fonseca, R., Víquez-García, L., & Rojas-Torres, L. (2021). Factores asociados al rendimiento académico en un curso de introducción a la estadística en Costa Rica. Épsilon, 109, 7-29.
Ureña. J. (2021). Representaciones de generalización & estrategias empleadas en la resolución de tareas que involucran relaciones funcionales. Una investigación con estudiantes de primaria & secundaria. [Tesis de doctorado, Universidad de Granada]. Repositorio Kerwá.
Virkki, O. T. (2022). Reasoning Skills Assessment in Information Technology National Entrance Examination Reform; a Design Science Approach. IEEE Global Engineering Education Conference (EDUCON), 719-7260. https://doi.org/10.1109/EDUCON52537.2022.9766817
Vista, A., & Alkhadim, G. S. (2022). Pre-university Measures and University Performance: A Multilevel Structural Equation Modeling Approach. Frontiers in Education, 7. https://doi.org/10.3389/feduc.2022.723054
Wilson, M., De Boeck, P., & Carstensen, C. H. (2006). Explanatory Item Response Models: A Brief Introduction. En J. Hartig, E. Klieme y D. Leutner (Eds.), Assessment of Competencies in Educational Contexts, (pp. 83-110). Hogrefe & Huber Publishers.
Wise, M. J. (2020). The Effective Use of Negative Stems and “All of the Above” in Multiple-Choice Tests in College Courses. Journal of Education Teaching and Social Studies 2 (4), 47-58. https://doi.org/10.22158/jetss.v2n4p47
